Gauss's Area Calculation Formula

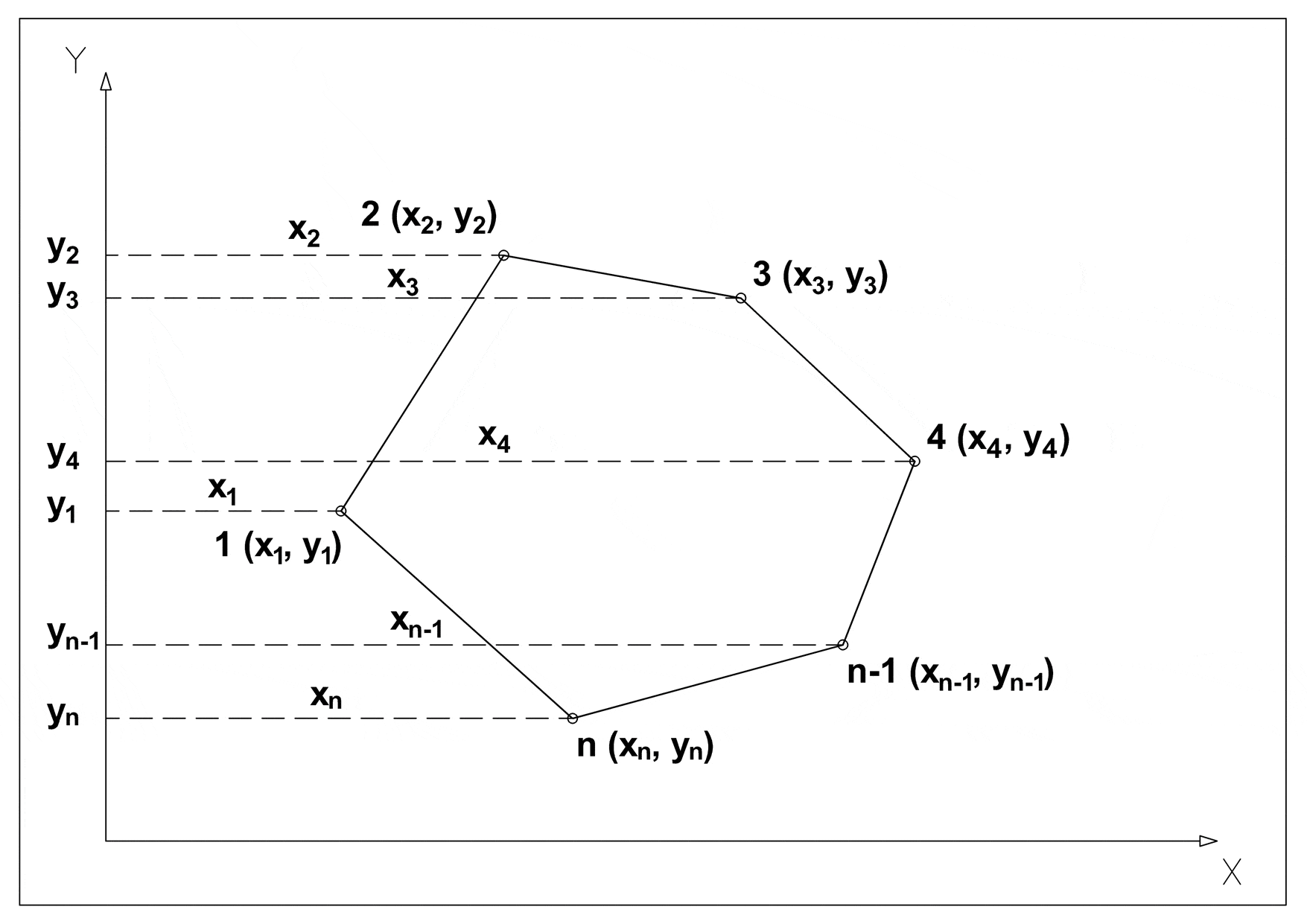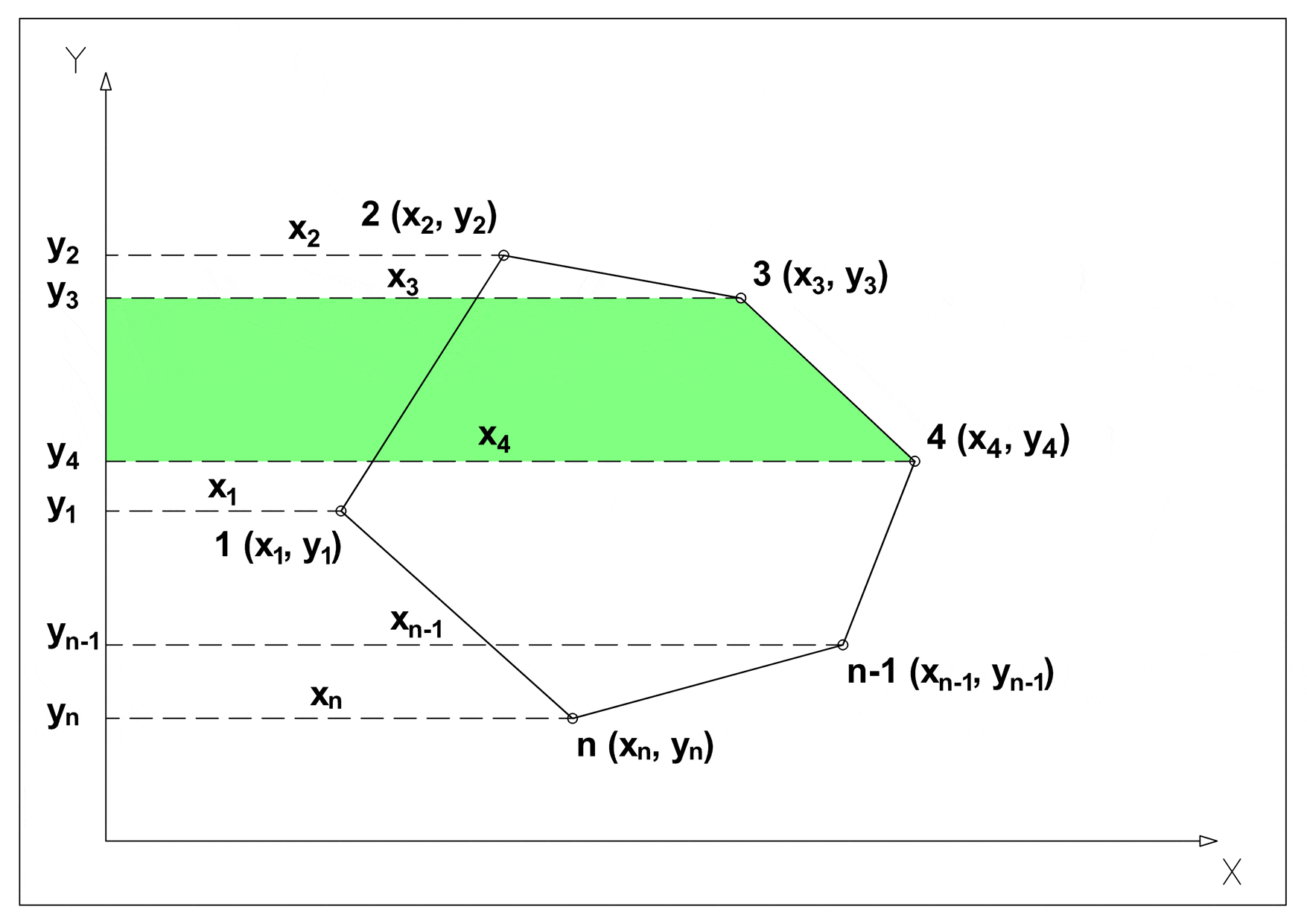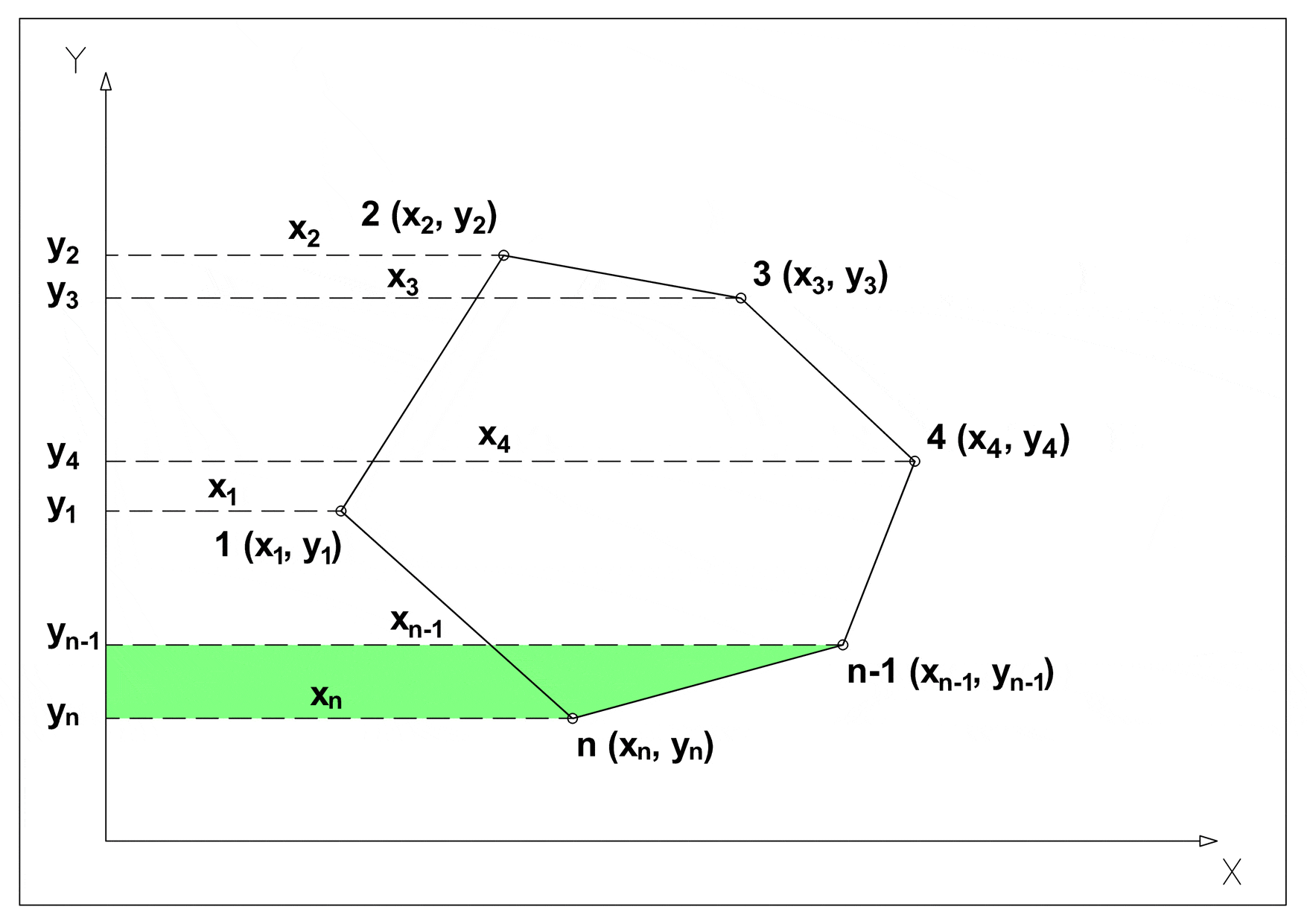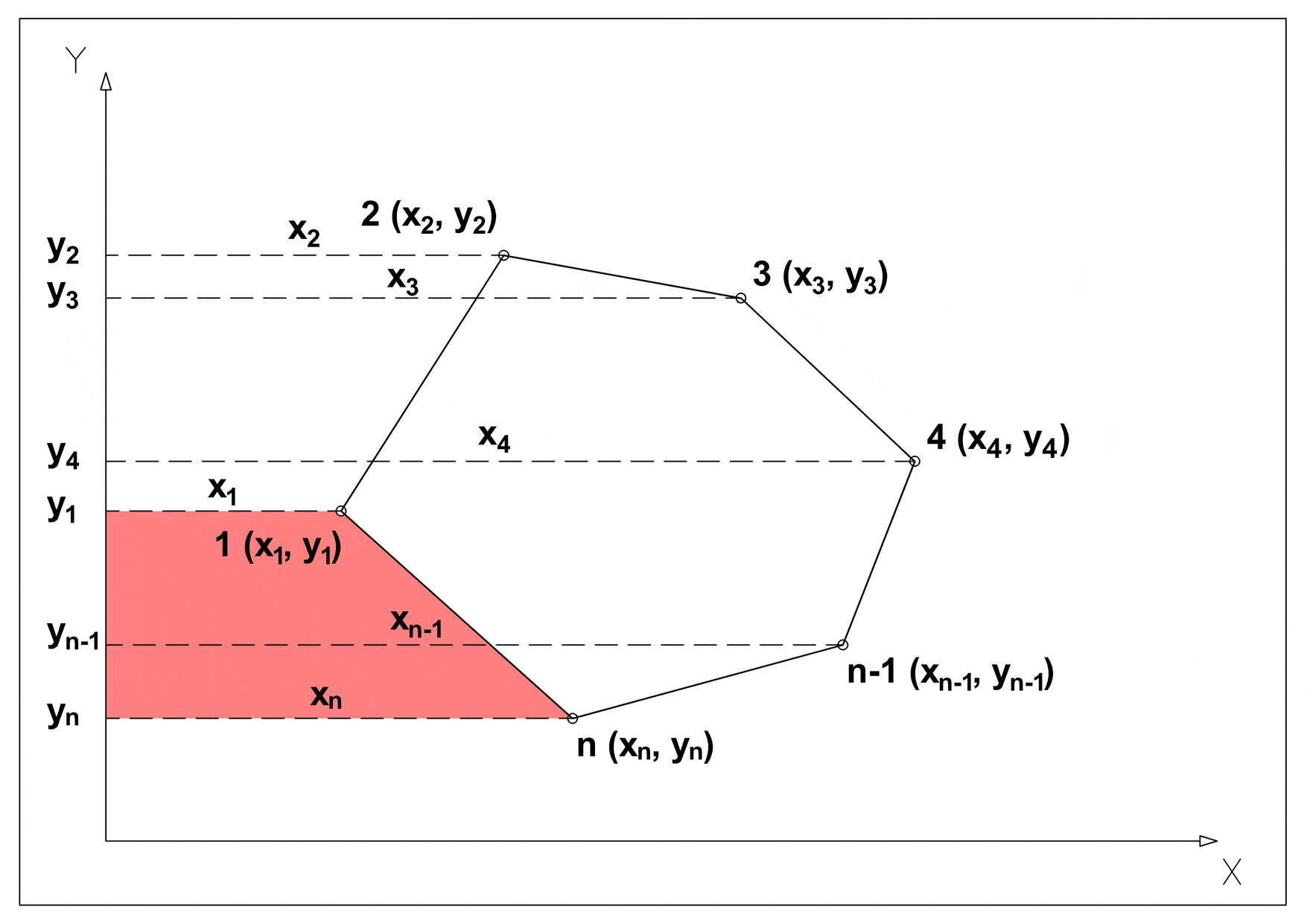
Calculate the surface area of a simple (non-self-intersecting) n sides polygonal shape with known Cartesian coordinates in the plane for all of its vertices. The main concept of the method is to divide the main polygon in n trapezoids and to cross-multiply corresponding coordinates to find the area enclosing the polygon (green trapezoids), and subtract from it the surrounding trapezoids (red) to find the area of the polygon within. It is also called the shoelace formula because of the constant cross-multiplying for the coordinates making up the polygon, like tying shoelaces. Mainly applicable in topography.

Known values: Cartesian coordinates of all vertices (x₁, y₁), ₍x_2, y₂), …(x_n, y_n).

Solution: Area A of simple polygonal shape.

 1. Subtract surrounding trapezoids (red) from encompassing trapezoids (green).

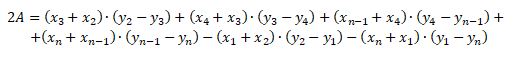
 2. In general:

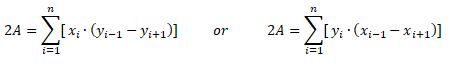
 where

• A is the area of the polygon,
• n is the number of sides (or vertices) of the polygon,
• x_i, y_i, i=1, 2, …, n are the Cartesian coordinates of polygon’s vertices, and
• +1 or -1 define next or previous vertex from i vertex.

If vertices are numbered clockwise, the determinants of the expressions above are positive whereas if numbered counterclockwise, they are negative in which case absolute values should be considered.