Calculation example - Calculate the height of an object when its base is inaccessible #2
Contents [show]
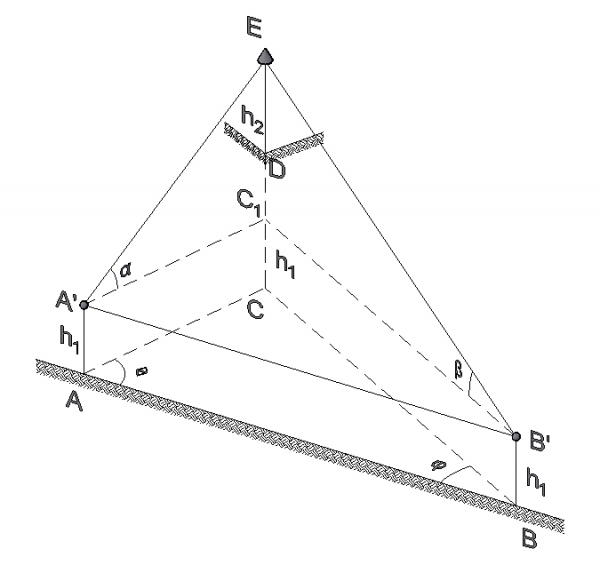
Calculate the height of an object from a baseline when its projected position to the ground is inaccessible. Case scenario when baseline AB is level but not in line with object.
Known values: Baseline distance AB length, height h1 of the observer at points A and B,
Angles measured at A – Horizontal angle θ and vertical angle α
Angles measured at B – Horizontal angle φ and vertical angle β.
Solution: Height of object above ground at position A.
In triangle ABC, given the sine law:
Then
Also
Thus:
Ηeight of object (Ε) above ground at station A = C1E + h1
and
Ηeight of projection (D) above ground at station A = C1E + h1 - h2 if height h2 is known.
Selected Topics
Want to read more like this?
Calculation example - Calculate the height of an object when its base is inaccessible #4
Jun, 26, 2019 | EducationCalculate the height of an object from a baseline when its projected position to the ground is inacc...

Calculation example - Calculate the height of an object when its base is inaccessible
Apr, 19, 2019 | EducationCalculate the height of an object from a baseline when its projected position to the ground is inacc...
Calculation example - Calculate the height of an object when its base is inaccessible #3
Jun, 26, 2019 | EducationCalculate the height of an object from a baseline when its projected position to the ground is inacc...
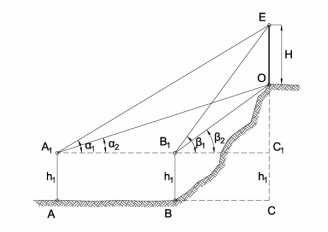
Calculation example - Calculate the height of an object when its top and bottom are visible but inaccessible
Jun, 26, 2019 | EducationCalculate the height of an object from a baseline when its top and bottom is visible but not accessi...

Calculation example - Calculate the height of an object when its top and bottom are visible but inaccessible #2
Oct, 18, 2019 | EducationCalculate the height of an object from a baseline when its top and bottom is visible but not accessi...

Calculation example – Calculate the height of a building - 2
Mar, 19, 2019 | EducationCalculate the height of a building where the ground is sloping up or down from the observer. Know...
Calculation example - Calculate the height of an object from three angles of elevation
Jan, 20, 2020 | EducationCalculate the height of an object by measuring three angles of elevation only, from stations A, B an...

Calculation example – Calculate the height of a building
Sep, 22, 2017 | EducationCalculate the height of a building by observing its top from two ground points and measuring corresp...

Calculation example - Calculate inclined angle of a bend
Jan, 20, 2020 | EducationCalculate the inclined angle φ of a bend along a bended path. Known values: Horizontal angle...
Trending

Calculation example - Three Point Resection

Calculation example - Determine the water content within a soil sample

Gauss's Area Calculation Formula

The history of the Golden Gate Bridge

Kallanai Dam (Grand Anicut)
Calculation example – Road design– Circular arc implementation

Minoan Water Harvesting and Distribution (Terracotta Pipes)

