Calculation example – Re-establishing an inaccessible Reference Station

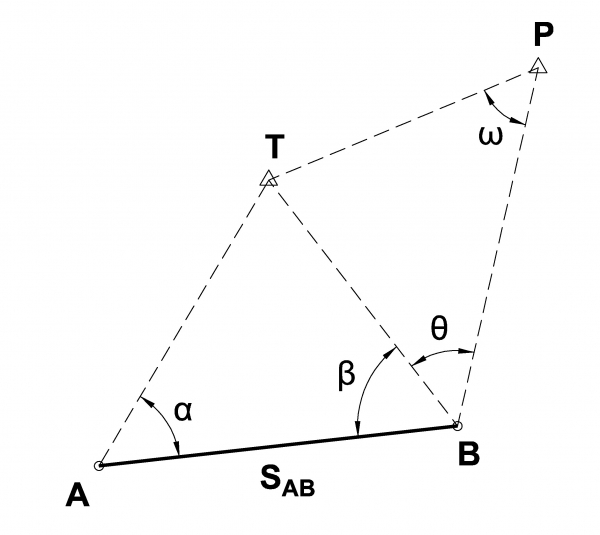
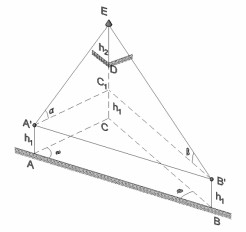
Re-establish the reference station T (inaccessible by the surveyor) onto position B and calculate the coordinates of stations A and B.

Known values: Angles α, β and θ – Distance (ΑΒ) – Coordinates (X_T, Y_T) and (X_P, Y_P).

Solution: Coordinates (X_A, Y_A) and (X_B, Y_B)

A second reference station P is far but visible from T and B. By occupying station A, measure angle α. From station B, measure angles β and θ. Finally, measure distance S_AB.

1. By applying the Second Fundamental Surveying Problem and the known coordinates of reference stations T and P, calculate the bearing angle TP and distance S_TP:

2. By applying the sine law on triangle TAB, calculate the auxiliary distances S_TA and S_TB:

3. By applying the sine law on triangle TΡΒ, calculate angle ω:

4. Then, calculate bearing angles α_TA and α_TB:

5. Considering the known coordinates of reference station T and applying the equations of the First Fundamental Surveying Problem:

6. For validating the results, apply the following: